DFS and BFS

1. A presentation about the difference between breadth first search and depth first search on a binary tree

• Breadth first search (BFS) the traversal of the graph's levels by exploring all the node's children before moving on to the neighboring node in a graph from left to right. Depth first search (DFS) is the traversal of nodes that prioritizes the furthest node before backtracking to other unvisited nodes from left to right. BFS utilizes the stack while DFS utilizes the queue to keep of unvisited nodes. They are both useful algorithms but both have their pros and cons.

• The breadth first search algorithm is useful for garbage collection in compilers while the depth first search algorithm is useful to create games like maze or Sudoku.

• They are both important algorithms for computer science in general. They are many different algorithms to learn but BFS and DFS are very common. It will likely be asked in job interviews to demonstrate the interviewee's problem solving ability.

2. An example of the DFS Algorithm Without Recursion

Code

• The linked code above is about finding the boolean value for True on a 2D grid. We use a randomly generated 2D coordinate for the value True. There can be only one True while the rest are all False. It looks something like this:

False False   False  False

False False **True** False

We use a directional vector (two arrays with specified x and y values) prioritizing depth over breadth as we traverse through the grid until we find the coordinate for True. It uses a stack to emulate the DFS algorithm by pushing unvisited nodes which are later popped when they are visited.

• This is used as the basis for a variant of the game Snake. It could also be used to create a Minesweeper game by having directional arrays be ideally randomly generated to emulate that of machine learning.

• It paves the way by helping provide a rudimentary sketch in preparation for other 2D based AI applications. It is a good prerequisite before learning about the OpenAI Frozen Lake gym environment.

DFS without recursion's pseudo-code looks like this:

func DFS_NO_REC(root)

  # Initialize a stack with the root node to start DFS
  STACK stack = [root]

  # Initialize a set to keep track of visited nodes to avoid revisiting nodes
  SET vis

  # Loop until there are no more nodes in the stack
  while (stack is not empty) do

    # Pop the top node from the stack (LIFO) to process it
    current_node = stack.pop()

    # Check if the node has not been visited
    if current_node not in vis then
      # Mark the current node as visited by adding it to the vis set
      vis.append(current_node)
    end if

    # Iterate over each child of the current node
    for each child in current_node.children do

      # If the child has not been visited, add it to the stack for future processing
      if child not in vis then
        stack.append(child)
      end if

    end for

  end while

  # Return the list of visited nodes
  return vis

END DFS_NO_REC

3. An example of the DFS Algorithm with Recursion

Code

• The linked code above is very similar to the previous project. But the difference mostly lies in the interactive side of things. It is a gambling game on a 2D grid that first asks the user to type a random number from 1 to 9. The program creates a random coordinate for the user's number and traverses through the grid until the user's number is found. It returns the total sum of the score based on the numbers traversed through the grid. The grid in question may look like this:

1   3   9

3 **4** 8

6   3   9

Instead of relying on a stack to keep track, we use a call stack traversing the grid recursively until the condition to find the user's number is met.

• It can be used in many random-based applications. There can be a terminal-based interactive game that involves decision making with each number from 1 to 9 meaning something. It can also be used to emulate dice.

• It is another reinterpretation of the DFS algorithm done differently. It is more concise than the stack approach.

DFS with recursion's pseudo-code looks like:

func DFS_REC(root, visited)

  # Add the current node to the visited set to mark it as visited
  visited.append(root)

  # Visit all unvisited child nodes recursively
  for child in root.children

    # If the child has not been visited yet
    if child not in visited
      # Recursively call DFS on the unvisited child
      DFS_REC(child, visited)
    end if

  end for

END DFS_REC

4. An example of the BFS Algorithm

Code

• The linked code above is about finding an English word in a JSON dictionary. It uses a queue until we return a valid word found in the dictionary. Misspellings are taken into consideration as it iterates the English alphabet until a valid word is found. BFS is emulated by having each word have its own valid child variants (In the case of cat, its valid variants from the dictionary are bat, bag, and cat. Together they are level one). We proceed to generate variants of each word respectively. The following picture provides a general overview being represented as a tree.

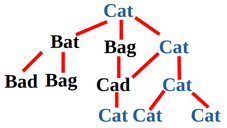
• It can be extended to other Latin-based languages like French or Malay. It can be a good application to find the distance between different words in a dictionary.

• The Breadth first search teaches a different to traverse graphs aside from depth first search.

BFS's pseudo-code looks like this:

func BFS(root)

  # Initialize a queue with the root node as the starting point
  QUEUE queue = root
  
  # Initialize a set to keep track of visited nodes to avoid cycles
  SET vis

  # Loop as long as there are nodes in the queue
  while (queue is not empty) do

    # Dequeue the first node (FIFO) to process it
    current_node = queue.pop()

    # Mark the current node as visited if it hasn't been visited already
    if current_node not in vis
      vis.append(current_node)
    end if

    # Iterate through each child of the current node
    for child in current_node.children

      # If the child node has not been visited, add it to the queue
      if child is not in vis
        queue.append(child)
      end if

    end for

  end while

end BFS

5. Explaining the A* Star Search Algorithm

Code

• The A-star algorithm can be like breadth first search but with distance and/or weight in mind. Instead of a queue, it is the priority queue that is relied upon. It is made to find the shortest path from point A to point B.

• It uses the following equation:

$$ f(n) = g(n) + h(n) $$

Where: $f$ is the total cost --- $g$ is the distance (or cost) --- $h$ is the heuristic value

• It is an ideal algorithm to create a GPS system. Anything that involves cartographic solutions or a system that is related to geography or geology may require such algorithm.

• The A* Star Search Algorithm provides a good sense of how destinations or vantage points are calculated and resolved. It is a more practical approach against breadth first search.

The A* pseudo-code looks like this:

func A_star(start, goal)

  # Initialize open list (priority queue) and closed list (set)
  OPEN_LIST = priority queue with start node, sorted by f value
  CLOSED_LIST = empty set

  # Initialize g and f values for the start node
  g(start) = 0
  f(start) = heuristic(start, goal)

  # Initialize a map to keep track of the parent of each node
  PARENT = empty map

  # Loop until the open list is empty
  while OPEN_LIST is not empty do

    # Get the node with the lowest f value from the open list
    current_node = OPEN_LIST.pop()

    # If the current node is the goal, reconstruct the path and return it
    if current_node == goal then
      return reconstruct_path(PARENT, goal)

    # Add the current node to the closed list
    CLOSED_LIST.add(current_node)

    # For each neighbor of the current node
    for each neighbor in current_node.neighbors do

      # If the neighbor is in the closed list, skip it
      if neighbor in CLOSED_LIST then
        continue

      # Calculate tentative g value for the neighbor
      tentative_g = g(current_node) + cost(current_node, neighbor)

      # If the neighbor is not in the open list or the new tentative g value is better
      if neighbor not in OPEN_LIST or tentative_g < g(neighbor) then

        # Update g and f values for the neighbor
        g(neighbor) = tentative_g
        f(neighbor) = g(neighbor) + heuristic(neighbor, goal)

        # Set the parent of the neighbor to the current node
        PARENT[neighbor] = current_node

        # Add the neighbor to the open list if it's not already in it
        if neighbor not in OPEN_LIST then
          OPEN_LIST.push(neighbor, f(neighbor))

      end if

    end for

  end while

  # Return failure if no path is found
  return failure

end A_star

# Helper function to reconstruct the path from start to goal
func reconstruct_path(PARENT, goal)
  path = empty list
  current_node = goal
  while current_node in PARENT do
    path.append(current_node)
    current_node = PARENT[current_node]
  end while
  reverse(path)
  return path
end reconstruct_path

Markov Decision Process (MDP) and Q-Learning

6. Explaining the Markov Decision Making Process

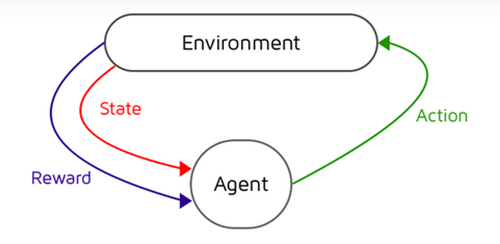
• The Markov framework is not the same as machine learning as it is a mathematical framework that enables computers to make decisions based on probabilities. It relies on 4 variables with Bellman's equation in mind. We use the equation to calculate the next possible action for the agent.

• Its outcomes are partly random and partly under the control of the decision maker. It provides a mathematical model for decision-making under uncertainty.

• Any agent or model can be used to emulate the Markov Decision Making Process. It loops until it finds the best possible solution or value to do something.

• It helps to teach the idea of the meaning behind word "agent", "cost", and "action space", and "observation space". Since AI heavily relies on mathematics, it can indirectly teach calculus as a bonus.

6.1 Bellman's Equation

It relies on 4 variables:

$$ (S,A,P_a,R_a) $$

Where:

• $S$ is the set of states called the state space. It is the "everything" that surrounds the agent.

• $A$ is the set of actions called the action space. It is the set of possible decisions that the agent can make.

• $P_a$ is the probability distribution of the next state given the current state and action. It is the transition model.

• $R_a$ is the immediate reward received after transitioning from the current state to the next state by taking action 'a'. It is the reward function.

We rely on these four parameters to create a model like so:

We then use Bellman's optimality equation in our code:

$$ V_{i+1}(s) := \max_a \bigg\{ \sum_{s'} P_a(s, s')(R_a(s, s') + \gamma V_i(s')) \bigg\} $$

With this equation, we keep looping, calculating and finding the most optimal value for the agent to commit an action. This is called value iteration.

Value iteration involves iteratively estimating the value of each state based on the rewards associated with taking different actions from that state. This allows us to find the best action to take in each state and ultimately determine the optimal policy. We iterate through all the states and update our estimates until we converge on the best policy.

7. Explaining the implementation of Markov Decision Making Process

The Frozen Lake OpenAI gym is a good example.

Implementation: Google Colab or Github

• By implementing the Bellman's equation as a Python function, the program will loop all of the available states and then calculate new values that will be compared against old values. It will keep looping until the difference between the old values and the new values will no longer be significant.

Note: It is just like finding the derivative of a function. The closer the derivative, the less significant it becomes.

def value_iteration(env, max_iterations=100000, gamma=0.9):
    """Determines how "good" any given state is to be in for our actor.

    Returns: an array with a value for each state, and another array for the policy.
        The greater a given value in the first array, the "better" the state.
    """
    # An array where each item represents how "good" a state is to be in
    state_func = [0] * env.nS
    # We'll update the state function gradually and use this copy to do it
    new_state_func = state_func.copy()
    # Our policy will contain the best action for any given state
    # Do this after the initial value iteration
    policy = [0] * env.nS

    # Prevent looping infinitely if our algorithm doesn't converge
    for i in range(max_iterations):
        # Loop through all possible states 
        #(n is the *S*tates. the *n*umber of *S*tates)
        for state in range(env.nS):
            # For each state we find the best possible action to take in that state
            best_state_action_val = 0
            # Do this after the initial value iteration
            best_action = 0
            # So we try all the actions
            for action in range(env.nA):
                state_action_val = calc_action_value(state, action, state_func, gamma)

                # After calculating the goodness of this action, we keep it only if it is
                # better than the previous best
                if state_action_val > best_state_action_val:
                    best_state_action_val = state_action_val
                    # Do this after the initial value iteration
                    best_action = action

            # After calculating the best possible action for this state, we save how
            # "good" the best action is for the state...
            new_state_func[state] = best_state_action_val
            # And we remember the action for later
            # Do this after the initial value iteration
            policy[state] = best_action

        # After 1000 iterations, if the state function hasn't improved very much
        # we stop trying to improve it
        if i > 1000 and sum(state_func) - sum(new_state_func) < 1e-04:
            break

        # Otherwise we update the state function to the newly improved version
        state_func = new_state_func.copy()

    # After figuring out the goodness of each state and the best actions we return them
    return state_func, policy

state_func, policy = value_iteration(env)
print(state_func)
print(policy)
print("Size of state_func", len(state_func))
print("Size of policy", len(policy))

• We then create a policy (or different possible outcomes) based on the new values for our agent to take a course of action through trial and error.

def get_score(env, policy, episodes=1000):
    misses = 0
    steps_list = []
    best_episode = []
    # We try to navigate the lake `episodes` number of times
    # "In other words, we're 'playing' this game episode number of times"
    for _ in range(episodes):
        # We reset the environment so we're back at the start, and store the current
        # state in `observation`
        observation = env.reset()
        episode = []
        steps = 0
        while True:
            # We use our policy to determine the best action based on the current state
            #"Given that I'm observing, what should I do?" 
            action = policy[observation]
            # We tell the agent to take the action and we retrieve the new state,
            # the reward for moving to that state, and also if we are done or not
            observation, reward, done, _ = env.step(action)
            # We'll save a string representation of the environment so we can watch
            # it later
            episode.append(env.render(mode='ansi'))
            steps += 1
            # If we finished and reached the goal
            if done and reward == 1:
                steps_list.append(steps)

                # We save this episode if we reached the goal in fewer steps
                if len(best_episode) == 0 \
                    or len(episode) < len(best_episode):
                    best_episode = episode

                break
            # If we finished but fell in a hole
            elif done and reward == 0:
                misses += 1
                break

    print('----------------------------------------------')
    print('You took an average of {:.0f} steps to get the frisbee'.format(
        statistics.mean(steps_list)))
    print('And you fell in the hole {:.2f}% of the time'.format(
        (misses / episodes) * 100))
    print('----------------------------------------------')

    return best_episode


best_episode = get_score(env, policy)

• It demonstrates a solid grasp of how the Markov Decision Making Process works. It is a solid impetus for a mathematical way of thinking.

8. Explaining the Q-Learning Reinforcement Learning

• We represent Q-Learning as a table called Q-Table.

• It is a table of action columns and state rows. Each state corresponding to a particular action can have a good or a bad "mark". We can still use Bellman's equation to help make such values.

• It is used on any agent just like in the Markov Decision Process. Unlike Markov Decision Making, it is not "pseudo-learning". The Q-table approach will be considered when the agent requires actual self-teaching unlike Markov's where probabilities don't deliver too much semantic significance reflecting on the environment the agent is in.

• It provides a new perspective to develop a reinforcement learning application.

8.1 The Q-table

It is one type of models to make a reinforcement learning program possible. We rely on a table with "grades" for every action for every state.

Every row is a state and every column (for this table, after first column) is an action. In the table, the possible grades are -10 meaning horrible, 5 is Good, while 10 is excellent.

Student	Listens	Writes	Interrupts
Not Available	-10	-10	-10
Available	10	5	-10

The Algorithm looks like

$Q(s)$: Returns the value of all actions for state s

$Q(s,a)$: Returns the value of the action a for state s

1. The agent goes through episodes/trials

2. Agent chooses the best value/best value:

$$ S \rightarrow max_a{Q(s,a)}=a\rightarrow S' $$

3. Update the cell: The reward tells us whether is was a good or a bad action (-10, 10, 5 etc.).

$$ Q(s, a)=r+\gamma \cdot max(Q(s')) $$

9. Explaining the Q-Table Implementation

The Taxi Driver OpenAI gym is a good example.

Implementation: Google Colab or Github

• Q-Learning helps the program generate a table of values for every state and action. In Python, we can use a table as a collection of tuples (state, action) to keep track (as from the example Q = np.zeros((env.nS, env.nA)), where Q holds the state nS and action nA).

• The Q-Learning way relies on a while loop until the agent reaches the destination. For every trial, the agent finds the best value with discount factor (represented as a gamma $\gamma$) as a coefficient to emulate that of the agent making progress. Through trial and error, the best possible moves are appended to the list.

Download PDF Download Text